Daten und Statistiken beeinflussen nicht nur unsere täglichen Entscheidungen, sondern spielen auch bei gesellschaftspolitischen Debatten eine  zentrale Rolle. Aus diesem Grund kommt der korrekten Vermittlung von Daten eine zentrale Rolle zu. Doch das ist einfacher gesagt als getan.
zentrale Rolle. Aus diesem Grund kommt der korrekten Vermittlung von Daten eine zentrale Rolle zu. Doch das ist einfacher gesagt als getan.
Der vorliegende Beitrag entstand 2023 im Rahmen der Sommerakademie «Stupid Statistics?!? Durchblick behalten im Daten-Dschungel der Gegenwart» der Schweizerischen Studienstiftung und wurde redaktionell begleitet von Reatch. Der Beitrag gibt die persönliche Meinung der Autorin wieder und entspricht nicht zwingend derjenigen von Reatch oder der Schweizerischen Studienstiftung. Erstmals erschienen im Reatch-Blog.
Statistik ist allgegenwärtig und überall auffindbar. Sei es beim morgendlichen Zeitungslesen, beim Online-Shopping oder im Strassenverkehr: Statistik begegnet uns jederzeit. Das Zusammentreffen von Mensch und Statistik kann dabei friedlich oder gar harmonisch sein, nicht selten zeugen jedoch Stirnrunzeln und Zähneknirschen von tiefgreifenden Konflikten zwischen Individuen und der mathematischen Datenanalyse. Gerade in einer sich schnell entwickelnden Informationsgesellschaft ist es aber von erheblicher Bedeutung, dass jede einzelne Person grundlegende Konzepte der Statistik versteht [1].
Die Aufgabe der Statistik ist klar: Daten korrekt sammeln, analysieren, interpretieren und darstellen. Die Vermittlung von statistischen Informationen schliesst daran an und versucht, komplexe Analysen und Interpretationen von Daten so aufzubereiten, dass sie auch von Menschen ohne grosse statistische Expertise verstanden werden.
Statistiker*innen – und alle Menschen, die Daten generieren, verarbeiten und präsentieren – stehen nicht nur in der Pflicht, Daten zu produzieren, sondern auch verständlich zu kommunizieren. Sie übernehmen eine gesellschaftliche Funktion, wenn sie forschungsbasierte Erkenntnisse aufbereiten und präsentieren. Die effektive Vermittlung setzt einerseits voraus, dass das Publikum über ein Grundverständnis der Materie verfügt. Andererseits erfordert sie von den Expert*innen ein hohes Mass an didaktischer Kompetenz.
Das Zieldilemma dabei: Einerseits muss die Darstellung so gestaltet sein, dass sie für eine breite Öffentlichkeit zugänglich ist, andererseits darf die wissenschaftliche Integrität nicht verloren gehen. Die Schlüsselkomponente in diesem Prozess ist die Kommunikation. Um Statistiken greifbar zu machen, müssen sie in klaren Botschaften vermittelt und visualisiert werden, sodass sie einem breiten Publikum zugänglich sind. Trotzdem bleibt das Risiko von Fehlinterpretationen bestehen, sodass auch das Publikum ein Mindestmass an Datenkompetenz mitbringen muss. Dies zu fördern gehört ebenfalls zu den Aufgaben verantwortungsvoller Vermittlung von Statistik.
Es kommt nicht selten vor, dass falsch oder zumindest unvollständig interpretierte Statistiken zu schockierenden Headlines führen. So geisterte vor einigen Jahren die Aussage durch die Medien, dass der tägliche Konsum von 50 Gramm verarbeitetem Fleisch das Risiko von Darmkrebs im Dickdarm um 18 Prozent erhöht [2]. Die Prozentzahl an sich stimmte zwar, doch sie liess das individuelle Risiko grösser erscheinen, als es tatsächlich war. Denn das absolute Risiko, an Darmkrebs zu erkranken, erhöhte sich bloss um einen Prozentpunkt: Wer täglich 50 Gramm Speck isst, erhöht laut den Studienresultaten sein Darmkrebsrisiko von ungefähr 6 auf ungefähr 7 Prozent. Das ist ein Anstieg, der statistisch signifikant und auch klinisch relevant ist, aber weitaus weniger beängstigend klingt als der relative Anstieg des Darmkrebsrisikos um 18 Prozent.
Die korrekte Vermittlung sowie die verständliche Darstellung von statistischen Konzepten und Daten gehen aber über die Frage hinaus, ob man sich zum Frühstück eine Scheibe Speck gönnen sollte oder nicht. Auch für eine funktionierende Demokratie ist statistisches Wissen essentiell. Ein konstruktiver und gerechter Meinungsaustausch setzt voraus, dass Personen ihre Meinung selbständig bilden und weiterentwickeln können. Den Medien kommt dabei viel Gewicht zu. Einerseits bilden sich viele Personen erst durch die Behandlung einer Thematik von Seiten der Medien eine Meinung. Andererseits kann eine grosse Vielfalt an Medien in der heute digitalisierten Welt einen starken Einfluss auf die Meinungsbildung ausüben. Angesichts der Allgegenwart von Statistiken und Daten in gesellschaftspolitischen Debatten ist es umso wichtiger, dass auch Menschen, die im Medienbereich arbeiten, statistische Kompetenzen haben.
In vielen Berichten verbirgt sich eine Wahrscheinlichkeitsangabe von, zum Beispiel, möglicherweise verhinderten Unfällen, die ohne eine nähere Betrachtung der verwendeten statistischen Mittel polarisierend wirken kann. Eine solche Polarisierung der Gesellschaft durch einen Bericht mit einer Anzahl von monatlich 200 aufgenommenen Geschwindigkeitsübertretungen auf einer Strasse könnte einen Effekt bewirken, dass das Stimmvolk sich für strikte Massnahmen der Durchsetzung von Geschwindigkeitskontrollen einsetzen würde. Wenn man aber in Betracht zieht, dass dieselbe Strasse eine monatliche Verkehrslast von 300’000 Fahrzeugen aufweist und die durchschnittliche Übertretung der Geschwindigkeit sich auf etwa 2 km/h aufrunden lässt, klingen die anfänglichen 200 Fahrzeuge bereits nach einer weniger grossen, beziehungsweise nicht mehr nach einer negativ konnotierten Zahl.
Gleiche Überlegungen lassen sich analog auf Daten anwenden, die zum Beispiel während den Wahlkampagnen von einigen politischen Parteien verwendet werden. Je nach Darstellung einer Grafik oder einer Statistik kann der Effekt auf das Publikum schon im Voraus stark beeinflusst werden. So kann eine Statistik durch absichtliches Herauslassen einiger Fakten, die wichtig sind für eine vollständige, differenzierte Interpretation, eine gezielte, künstlich hergestellte Reaktion auslösen. Den Effekt kann man sich über das vorher genannte Beispiel mit Geschwindigkeitsübertretungen näherbringen. Als Faustregel könnte man festhalten, dass sobald eine Statistik etwas zu gut oder zu schlecht – also polarisierend – darstellt, der Effekt durch eigene Recherche überprüft werden sollte.
Der Knackpunkt einer Meinungsbildung liegt also nicht nur darin, welche Daten man verwendet oder mitbekommt, sondern wie man dieselben Daten interpretiert und analysiert. In anderen Worten: Es ist wichtig, wie die Daten vermittelt und verstanden werden. Es ist im Sinne einer Demokratie, dass sich Bürger*innen an politischen Diskursen informiert beteiligen können, um so auch den Durchblick nicht zu verlieren. Statistische Kompetenzen sind deshalb in der heutigen, datengetriebenen Welt nicht mehr wegzudenken, wenn es darum geht, Daten korrekt einzuordnen, zu interpretieren und zu vermitteln [3].
Aufgrund der Unabdingbarkeit der statistischen Kompetenzen ist es sinnvoll, Statistiker*innen bereits bei der Erstellung und im Nachhinein auch in der Darstellung von ausschlaggebenden Daten beizuziehen. Man könnte in einem Interview zusätzlich zu den Fachpersonen auch Statistiker*innen um ihre Meinung fragen. Auf unser Beispiel mit den Geschwindigkeitsübertretungen bezogen würde man nun nicht nur die Aussage eines oder einer Polizeiangestellten erheben, sondern parallel dazu auch die Auslegung des Resultats der Messungen von einer Statistikerin oder einem Statistiker hinzufügen, um eine möglichst nützliche Breite an Informationen an die Lesenden weiterzugeben. Somit wird dafür gesorgt, dass wichtige Daten nicht vergessen gehen und sich das Publikum anhand einer vollständigen Informationsbreite eine Meinung bilden kann. Eine Zusammenarbeit zwischen Statistiker*innen und Medienhäusern ergibt insofern Sinn, um eine gewisse Überwachung von den zu publizierenden Daten zu gewährleisten und die Qualität und die Aussagekraft der publizierten Artikel zu sichern.
Damit ein möglichst breites Publikum von statistischen Kompetenzen profitieren kann, sollte auch das Bildungssystem dementsprechend angepasst werden. Angewendet auf das Schweizerische Schulsystem sollte deshalb eine grundlegende statistische Bildung während der obligatorischen Grundausbildung sichergestellt werden. Für das Schulwesen sind die Kantone zuständig [4], weshalb es auch in deren Obhut liegt, statistische Grundlagen in den obligatorischen Schuljahren sicherzustellen. In Betracht auf die bisher aufgezeigten Gründe zur Nützlichkeit von statistischen Kompetenzen erscheint es durchaus sinnvoll, der Bevölkerung bereits in jungen Jahren ein gewisses Verständnis der Statistik beizubringen, auch wenn komplizierte mathematische Formeln ausgelassen werden (müssen), um didaktisch sinnvoll zu bleiben. Es würde bereits ausreichen, wenn Kinder und Jugendliche verstehen, wie gewisse Grundprinzipien funktionieren.
Zum Beispiel lassen sich Wahrscheinlichkeiten mit anschaulichen Strichfiguren darstellen. Angenommen, dass von 100 Personen 6 keinen Fernseher Zuhause haben. Dieses Verhältnis lässt sich über ein Bild mit 100 Personen darstellen, in welchem 6 Personen rot sind, also keinen Fernseher zuhause haben:

Zufälle lassen sich mit praktischen Beispielen wie Münzenwerfen oder Farbkugeln-Ziehen veranschaulichen. Auch die Bedeutung der Stichprobengrösse kann anhand eines illustrativen Beispiels mit demselben Farbkugeln-Ziehen demonstriert werden. Dafür kann man mehrere Stichproben aus einer Gesamtmenge an Farbkugeln erstellen. Man greife in einen Sack mit einem bekannten Verhältnis an Farbkugeln und verteile eine festgelegte Anzahl an zufällig gewählten Kugeln in mehrere kleinere Säckchen. Daraus zählen die Schüler*innen dann die Anzahl einer spezifischen Farbe. Je mehr Stichproben (kleine Säckchen) man erstellt, desto besser entsprechen die Resultate der realen Wahrscheinlichkeit, diese eine spezifische Farbe der Farbkugeln zu ziehen:
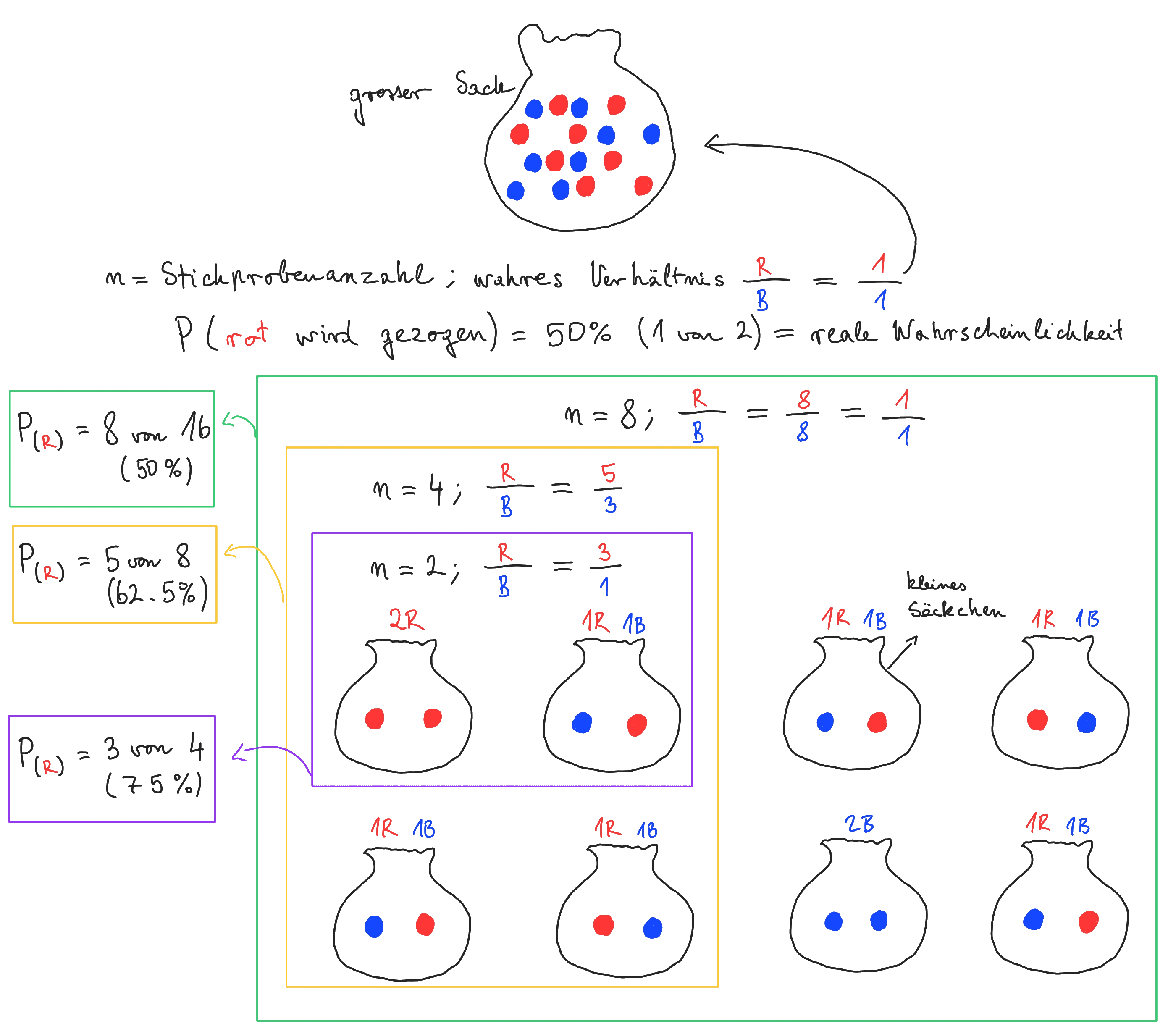
Mathematische Formeln halten sich bei den eben erwähnten Demonstrationen in Grenzen, da es dabei eher darum geht, Konzepte und Denkweisen beizubringen. Dabei bleibt das wohl wichtigste Konzept beim Verständnis von Statistik der kritische Umgang mit Daten. Es ist nun mal nicht alles genau so (einfach), wie es auf den ersten Blick erscheint. Ein solcher Gedankengang motiviert zur eigenständigen Recherche nach der Bedeutung der gelesenen Daten und bewirkt schliesslich ein besseres Verständnis von Daten und Statistiken.
Zwar dürfte die Umstellung der Lehrpläne einige Zeit in Anspruch nehmen und auch dann wären wir wohl noch weit entfernt von einer Gesellschaft, in welcher statistische Kompetenzen eine Selbstverständlichkeit sind. Doch der hier vertretenen Ansicht nach sollten Schritte in die beschriebene Richtung gemacht werden, damit nicht nur der Bildungsstand der Bevölkerung gesichert wird, sondern auch Institutionen wie unsere Demokratie langfristig geschützt werden.
Schlussendlich liegt es sowohl in der Verantwortung der Leser*innen als auch Statistiker*innen und Journalist*innen, Statistiken richtig zu verstehen und vor allem, Statistiken richtig zu vermitteln.
Quellen
Anhang
Je nach Darstellung der Daten aus statistischen Analysen wird auch die Interpretation derselben Daten beeinflusst. Statistische Mittel wie Relatives Risiko (RR) oder Relative RisikoReduktion (RRR) haben bei vielen Menschen eine zu starke Wirkung in der Interpretation, obwohl die absoluten Zahlen gleichzeitig gering bis insignifikant sein können. Auch das Absolute Risiko (AR) kann verwirrend sein und nicht genügend klar dargestellt werden. Es gibt noch die Darstellungsform “Number Needed to Treat” (NNT) und weitere.
Ein Beispiel zu absoluten und relativen Zahlen wird folglich hier aufgebaut [5].
Zur besseren Veranschaulichung der Formeln werden zusätzlich Strichfiguren verwendet. Eine Legende der Strichfiguren wird hier dargestellt:

In folgender Zeichnung soll Vegi bedeuten, dass verarbeitetes Fleisch nicht täglich gegessen wurde in den mit V markierten Stichproben (Kontrollgruppe), Speck soll die Stichproben darstellen, die verarbeitetes Fleisch täglich konsumierten:
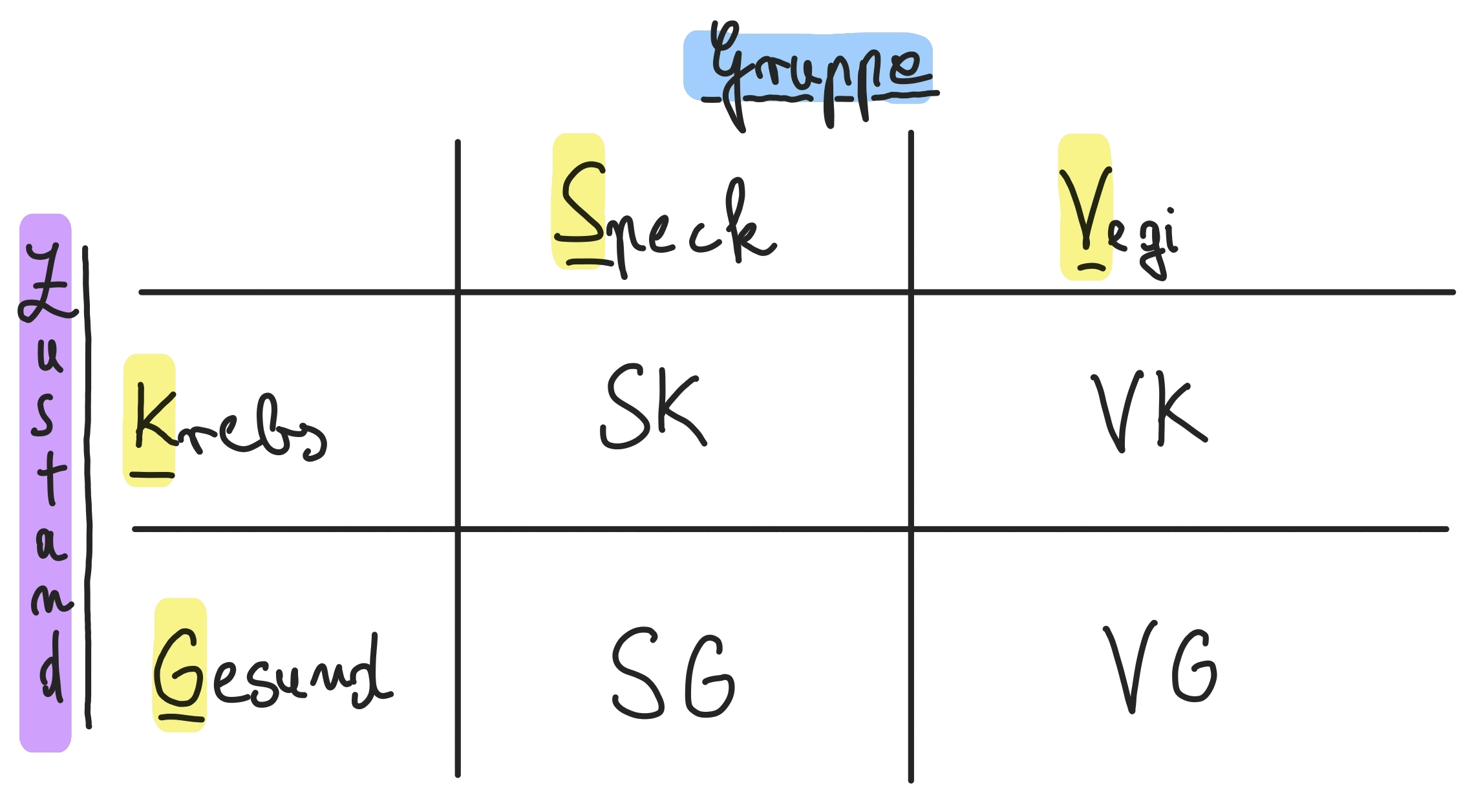
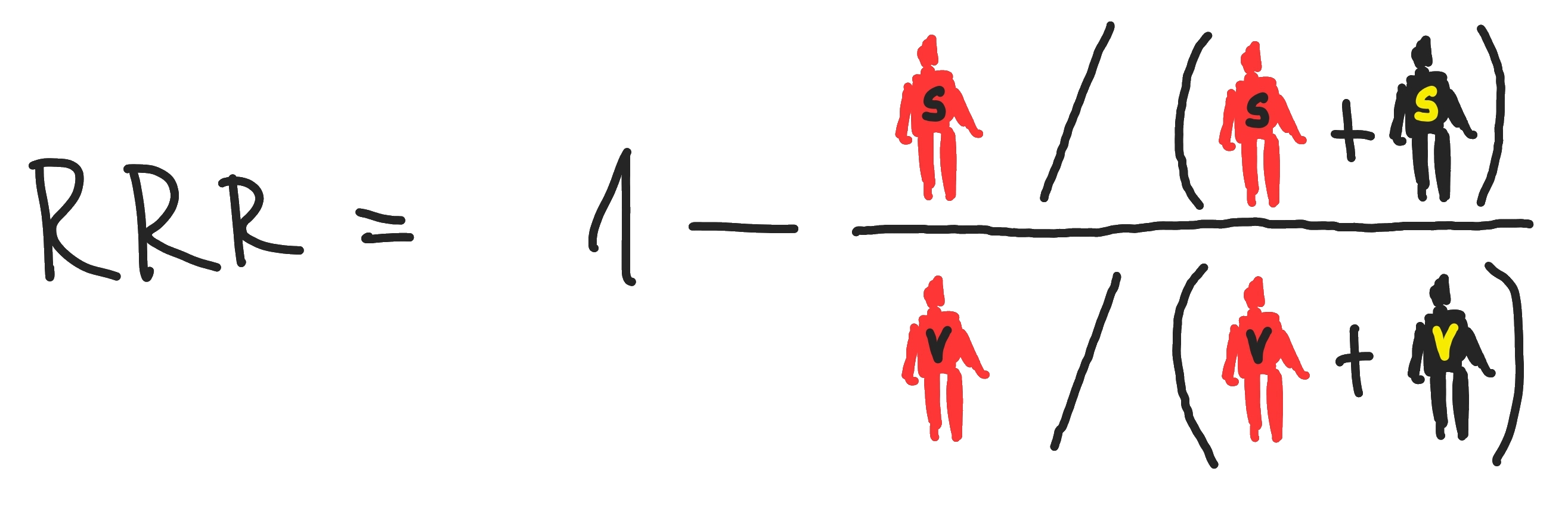
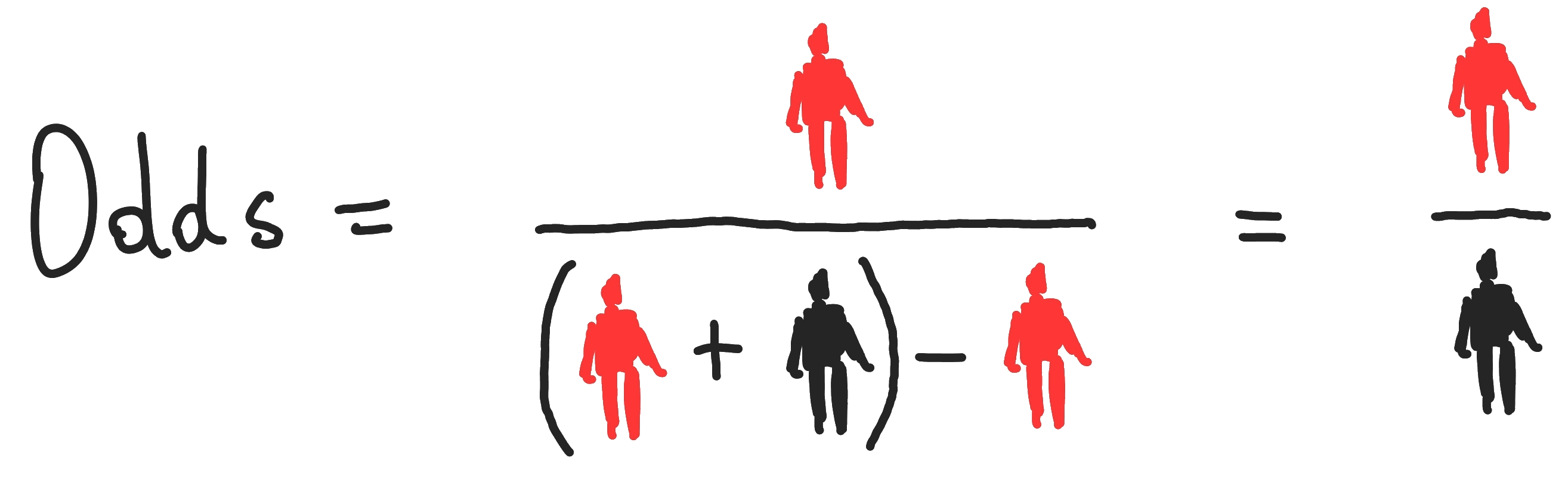
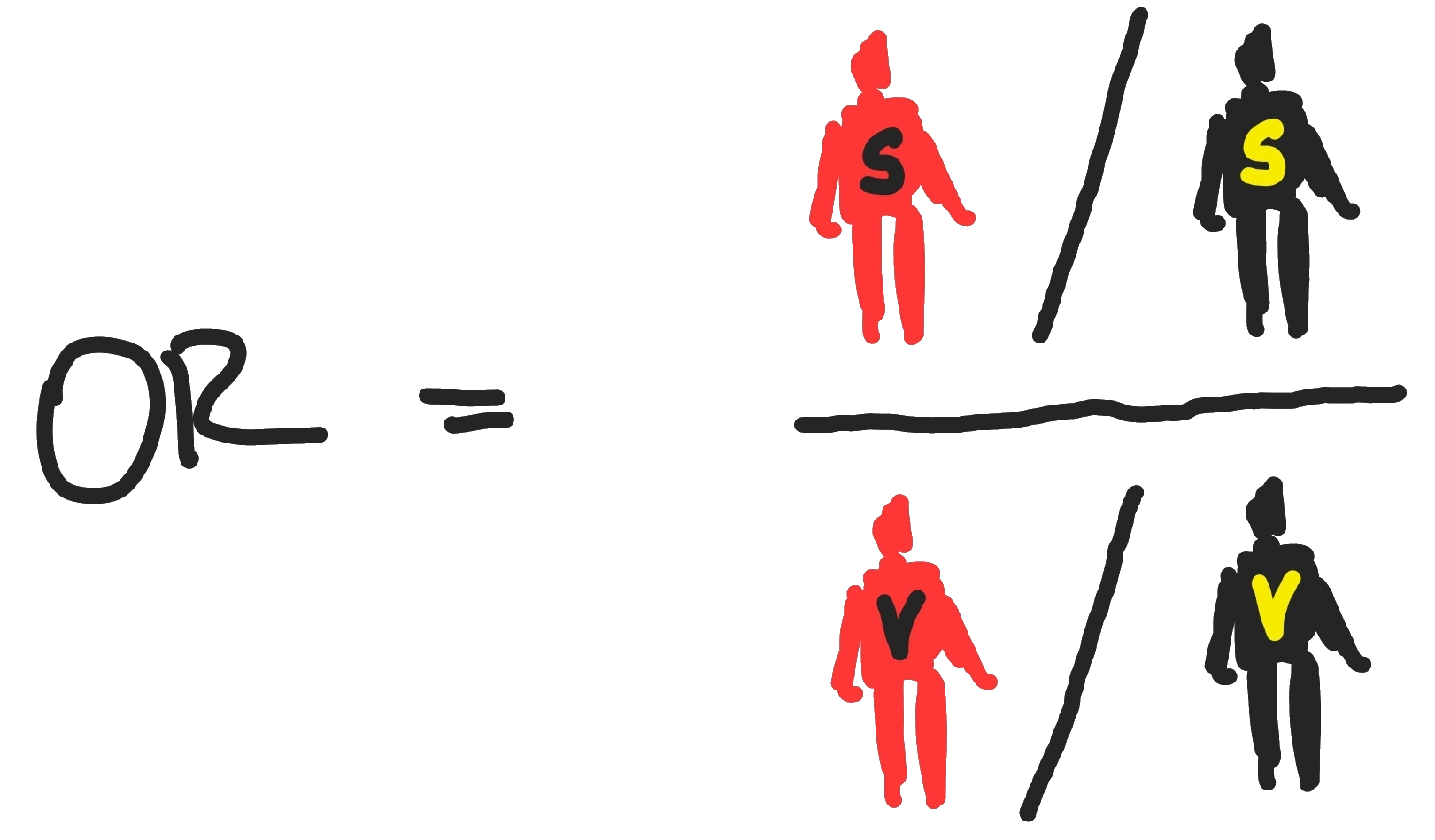
Die relevanten Formeln zum Verständnis der Entstehung von einigen relativen und absoluten Zahlen sind hier ersichtlich [6]:
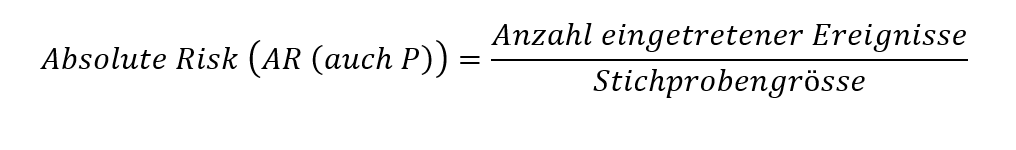


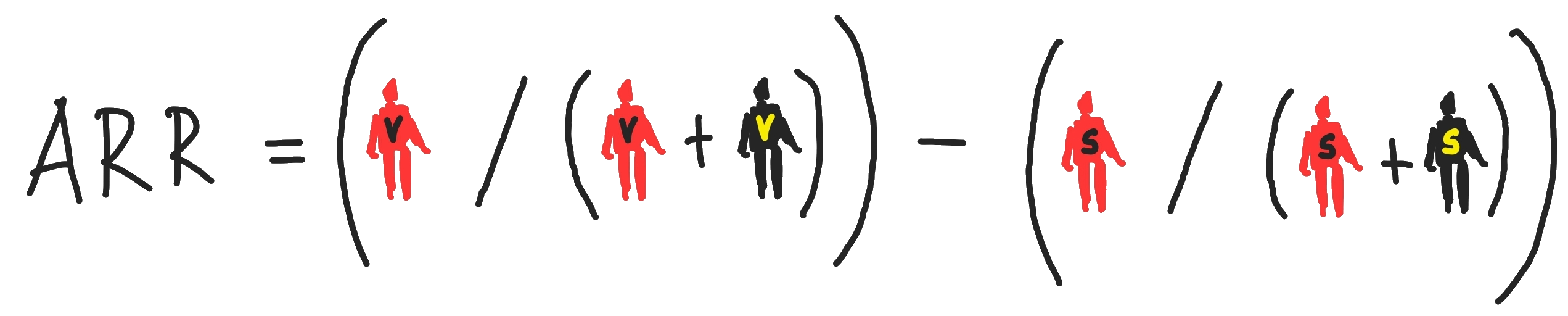

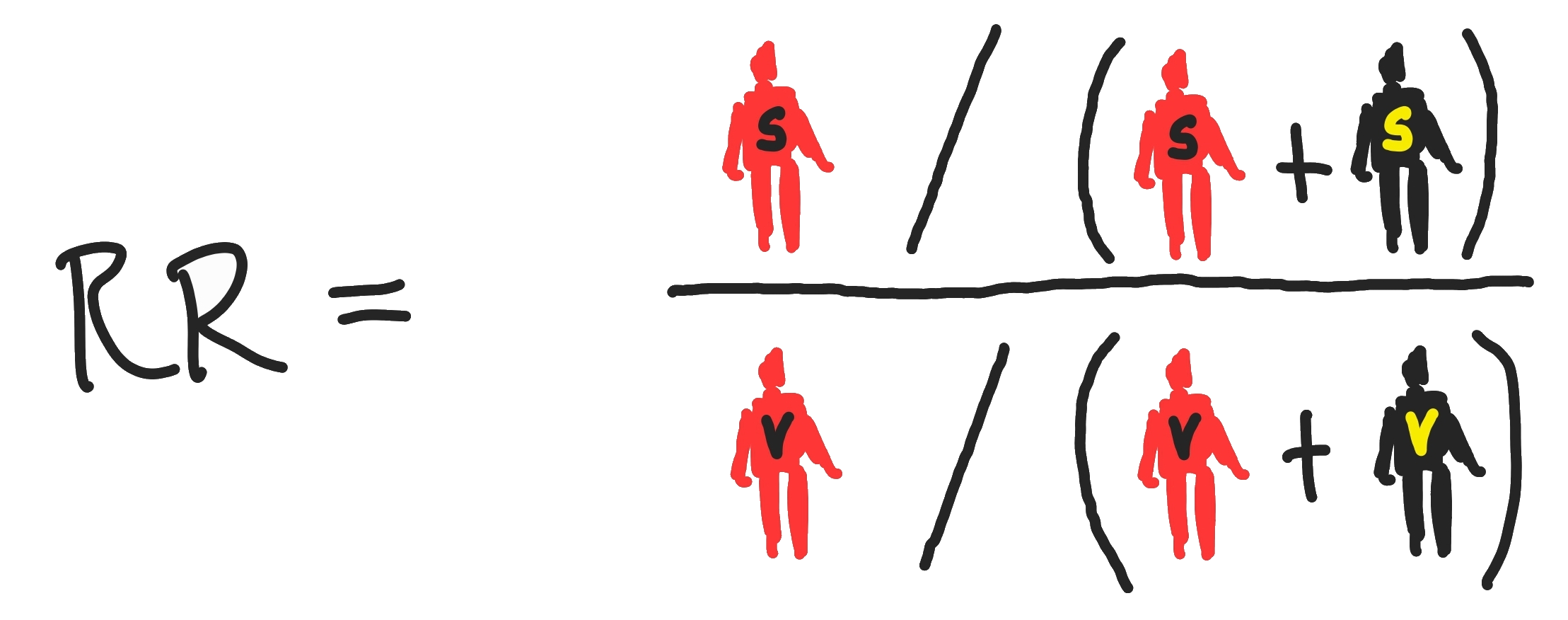


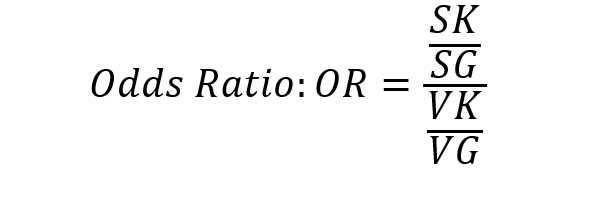

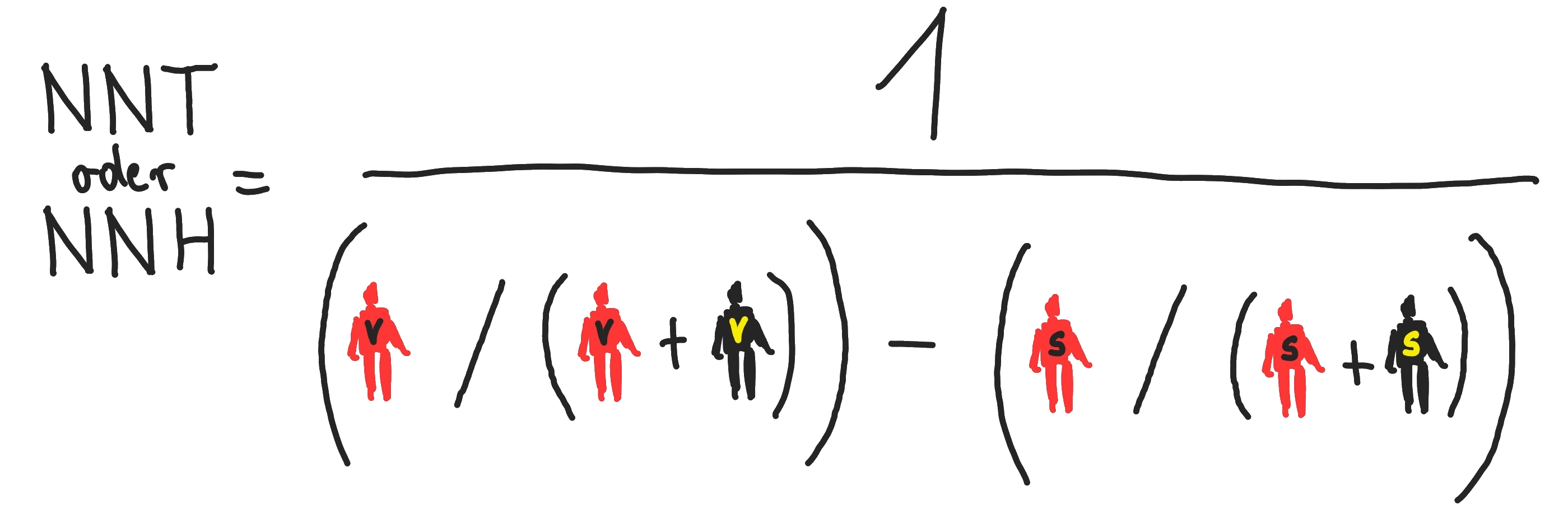
Bei der NNT kann man positive und negative Werte erhalten. Bei einem positiven Wert würde man folgenden Schluss ziehen: Damit eine Person weniger als in der Kontrollgruppe den untersuchten Effekt aufweist, müsste man die in der NNT berechnete Anzahl an Personen den experimentellen Bedingungen aussetzen.
Bei einer negativen NNT würde man hingegen folgenden Schluss ziehen: Damit eine Person mehr den untersuchten Effekt aufweist, müsste man die in der NNT berechnete Anzahl an Personen den experimentellen Bedingungen aussetzen. Dies wird oft als Number Needed to Harm (NNH) bezeichnet. Der Grund für den negativen Wert ist eine negative Absolute RisikoReduktion.
Ein konkretes Beispiel mit eingesetzten Zahlen wird anschliessend aufgebaut.
In folgender Zeichnung soll erneut Vegi bedeuten, dass verarbeitetes Fleisch nicht täglich gegessen wurde in den mit V markierten Stichproben (Kontrollgruppe). Speck soll die Stichproben darstellen, bei denen verarbeitetes Fleisch täglich konsumiert wurde. Beide Stichproben betragen jeweils 100 Testpersonen:
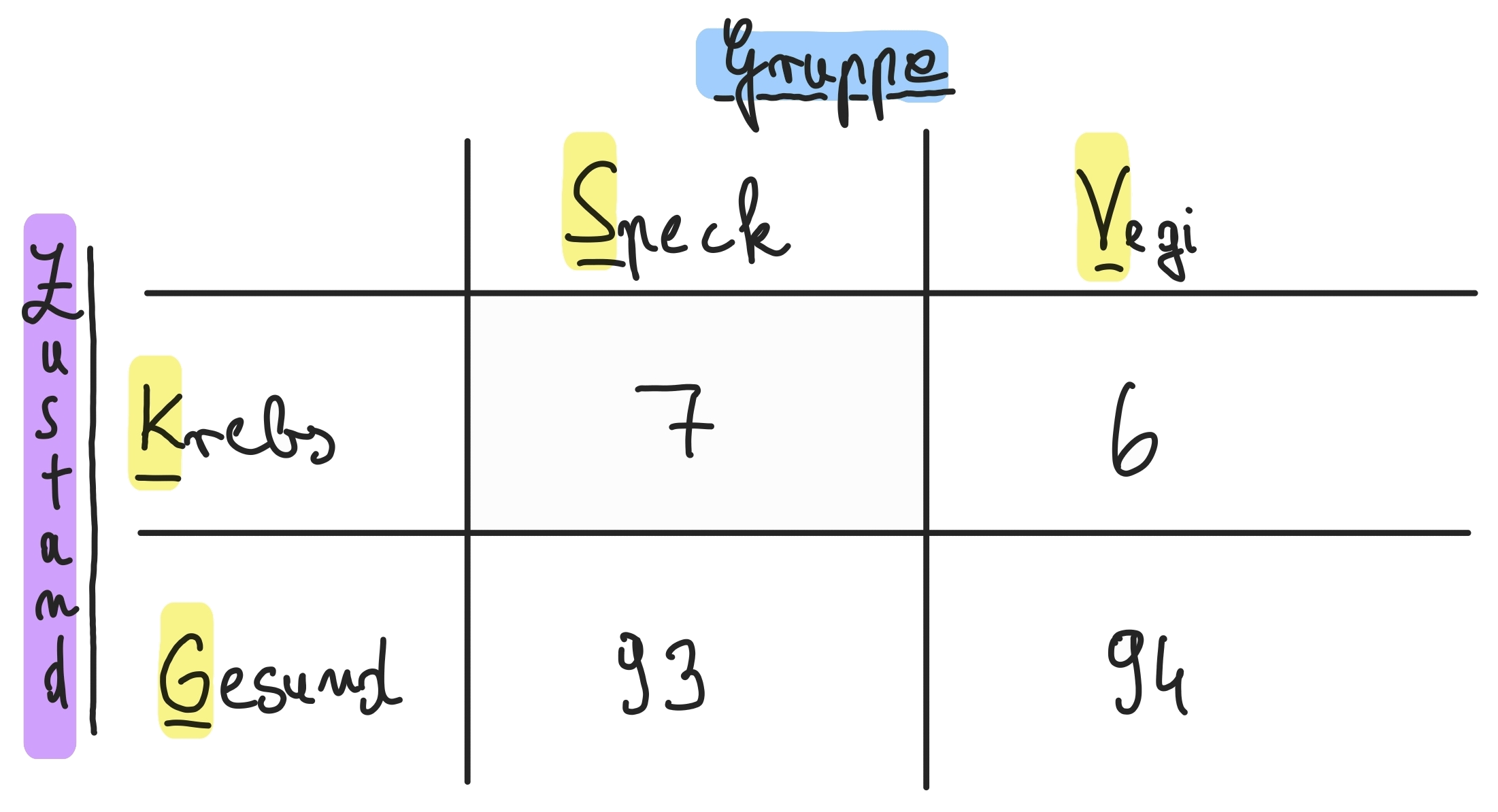
Aus der vorigen Tabelle werden nun statistische Berechnungen gemacht.
Wahrscheinlichkeit für Darmkrebs bei täglichem Speckkonsum:
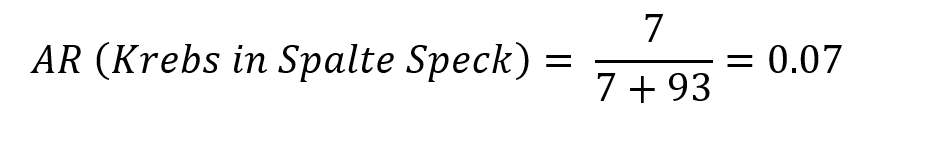
Wahrscheinlichkeit für Darmkrebs bei Kontrollgruppe:
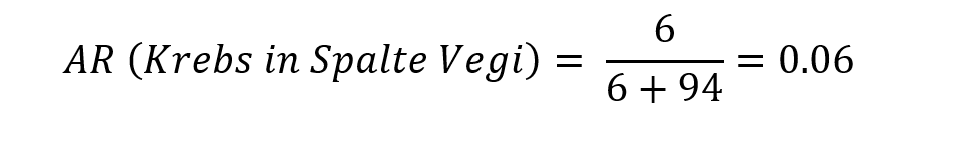
Absolute RisikoReduktion:
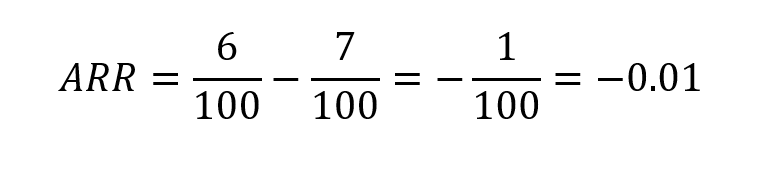
Die ARR ist im negativen Bereich. Das bedeutet, dass es sich nicht um eine Absolute RisikoReduktion handelt, sondern um eine absolute Risikozunahme.
Relatives Risiko:
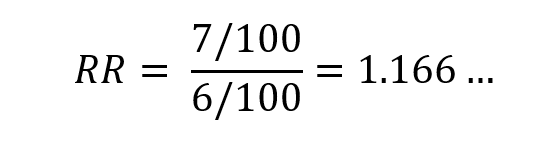
Relative RisikoReduktion:
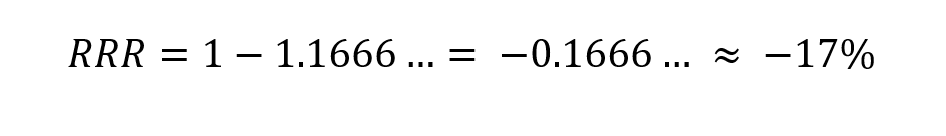
Die hier berechnete RRR ist erneut negativ. Es besteht also ein etwa 17% höheres Risiko an Darmkrebs zu erkranken aufgrund von täglichem Speckkonsum von 50g im Gegensatz zum Risiko für Darmkrebs ohne den erwähnten täglichen Speckkonsum. Die Relative RisikoReduktion ist aber in diesem Fall sehr leicht falsch zu interpretieren ohne die Erwähnung von den zwei absoluten Risiken, aus welchen diese Zahl hier berechnet wurde.
Odds für Darmkrebs bei täglichem Speckkonsum; respektive Darmkrebs in der Kontrollgruppe, sowie das entsprechende Odds Ratio:
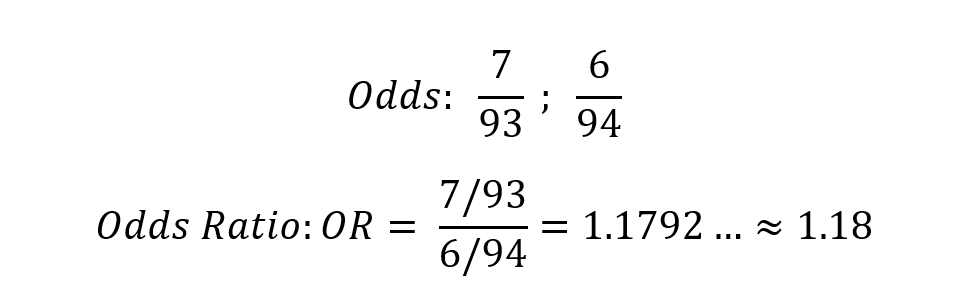
Auch die Odds Ratios sind leicht überzuinterpretieren, da sie eine ähnliche Aussage wie das Relative Risiko liefern. Hier ist das Resultat ohne die absoluten Risiken ebenfalls schwer interpretierbar.
Number Needed to Treat beziehungsweise Number Needed to Harm:
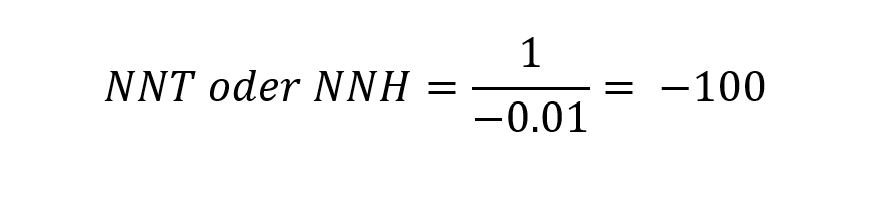
Den negativen Wert in der NNT kann man als NNH interpretieren. Die konkrete Aussage dieser Berechnung wäre also: Von 100 Personen, die täglich 50g Speck konsumieren, würde eine Person mehr an Darmkrebs erkranken, als in der Kontrollgruppe von 100 Personen, die keine 50g Speck täglich konsumieren. Eine anschauliche Variante der NNT ist die folgende Darstellung mit Strichfiguren:

Diese Darstellung beinhaltet sowohl die Wahrscheinlichkeit für Darmkrebs in der Kontrollgruppe, als auch die Wahrscheinlichkeit für Darmkrebs in der Experimentgruppe mit Speckkonsum von 50g täglich. Die Differenz dieser beiden Gruppen wird mit der violetten Strichfigur gezeigt. Das gelbe S auf der violetten Strichfigur deutet auf die Zugehörigkeit zur “Speckgruppe” hin. So anschaulich diese Darstellung auch sein mag, hat sie auch Nachteile. Konkret wurden in diesem Fall zwei rote Strichfiguren direkt nebeneinander gezeichnet, was zum Übersehen führen könnte beim Abzählen der Figuren. Allgemein müsste man bei solchen Darstellungen stets eine Stichprobenanzahl sowie die restlichen absoluten Werte (AR, ARR, …) kennzeichnen, da man sonst abzählen muss, welche Gruppe wie stark betroffen ist vom untersuchten Wert.
